2. La durée des vagues d’accélération
2.1 La durée des vagues d’accélération selon la méthode des moyennes mobiles
2.2 Les vagues d’accélération selon la méthode des courbes de tendance
3.1 Le cycle en cours et son évolution
3.3 Evolution des points hauts du cycle boursier
3.3.2 Les points hauts par cycle
3.3.3 Les points hauts des vagues d’accélération
4. Annexe : Mises à jour du onzième cycle
4.1 Les données au 30 octobre 2016
4.2 Le tableau d’ensemble au 30 octobre 2016
4.3 Le calcul des vagues d’accélération
4.3.1 L’évolution du rapport i/p selon la méthode des moyennes mobiles
4.3.2 L’évolution du rapport i/p selon la méthode de la tangente
1. Introduction
Selon notre analyse actuelle, à partir des données disponibles au 30 octobre 2016, nous serions entrés dans la phase du cycle qui précède la crise. Nous l’appelons, conventionnellement, « vague d’accélération ». Elle pose la question de sa durée puisque celle-ci détermine la prévision de la crise. La publication, fin août 2016 et révisées en septembre (et maintenues en octobre), par le BEA, des données du deuxième trimestre 2016, sont l’occasion pour rectifier la prévision. Sur la base des données disponibles au moment de la sortie du livre « le cycle des crises aux Etats-Unis depuis 1929 », les méthodes que nous avons développées pour anticiper le point de départ de la vague d’accélération, donc la dernière phase du cycle avant la crise de surproduction, désignaient le premier trimestre 2019. Compte tenu de la longueur potentielle d’une vague d’accélération, cela nous permettait d’escompter une crise de surproduction en 2019-2020. Les nouvelles données, publiées fin juin 2016, conduisent sur la base des mêmes méthodes à rapprocher de plus de deux ans la crise de surproduction. Dans ce texte, d’une part nous rectifions à nouveau la prévision, à la suite d’une erreur de calcul, et d’autre part, nous revenons sur la détermination de la durée potentielle de la vague d’accélération.
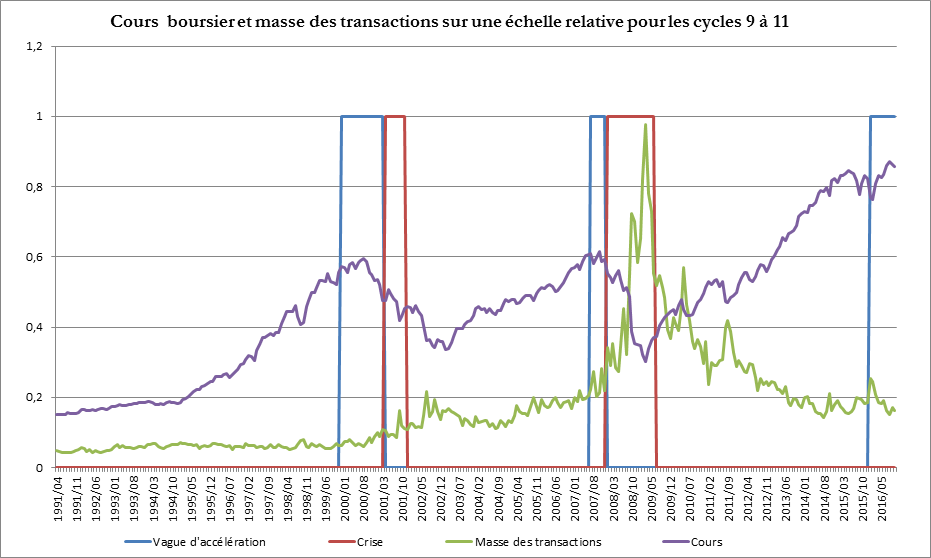
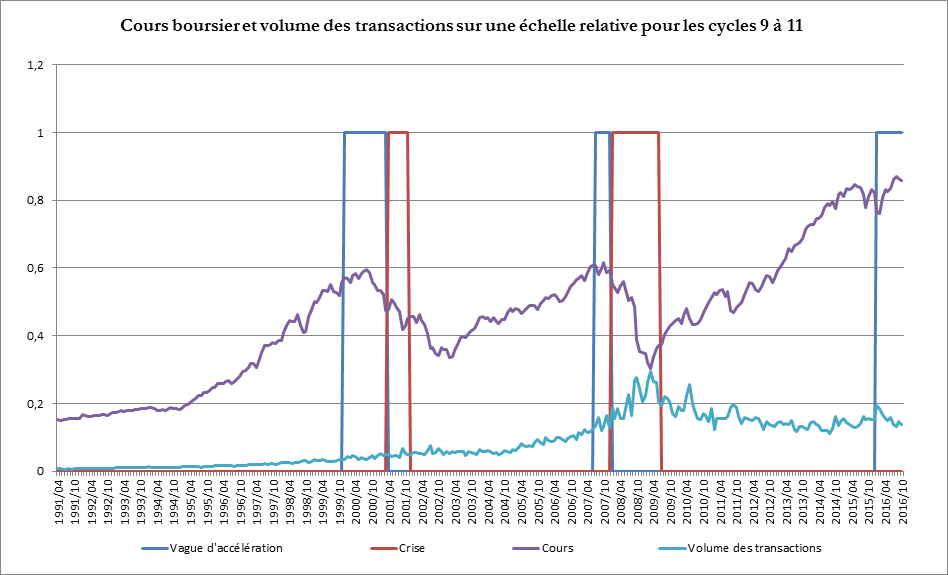
Comme nous l’escomptions, l’indice SP500 a battu son record historique. La nouvelle crise boursière qui est souvent le signe précurseur de la crise de surproduction aura donc lieu, cas le plus probable, pendant la vague d’accélération ou, sinon, une fois la crise de surproduction commencée (c’est ce qui est arrivé en 1929 ou encore lors du septième cycle). Dans ce dernier cas, cela signifierait l’ouverture d’une phase hyper spéculative d’entrée de crise. Cette phase du cycle, plutôt brève et rarement présente, est appelée hyper spéculative car elle intervient alors que les cycles du capital réel sont dans une période défavorable (période de crise pour le cycle des crises, période de contraction pour le cycle des taux et rapports) tandis que le cycle du capital fictif (cours boursier) est dans une période de progression. Bien que cette crise du capital fictif puisse contribuer à précipiter la crise de surproduction, son déclenchement effectif reste imprévisible. Nous ferons cependant le point sur l’évolution du cycle boursier.
2. La durée des vagues d’accélération
2.1 La durée des vagues d’accélération selon la méthode des moyennes mobiles
A partir des tableaux récapitulatifs présentés dans le document de présentation et de complément du livre (texte de juillet 2016), nous obtenons le tableau général suivant. Ce tableau reprend pour chaque série (taux et rapports) la durée de la dernière vague d’accélération, c’est-à-dire de la vague d’accélération qui débouche sur une crise.
Tpg : Taux de profit général
Tpe : Taux de profit d’entreprise
Tpva : Taux de profit sur la valeur ajoutée
Tplg : Taux de plus-value général apparent
Tplips : Taux de plus-value 2 (intérêt + profit / salaire)
Tplps : Taux de plus-value 3 (intérêt/profit)
Ip : Rapport Intérêt/Profit
Kp : Rapport Capital fixe/Profit
Synthèse : Durée de la vague issue de la confrontation des séries.
|
Cycle |
tpg |
tpe |
tpva |
tplg |
tplips |
tplps |
ip |
kp |
Synthèse |
|
2 |
9 |
9 |
9 |
9 |
9 |
9 |
6 |
8 |
6 |
|
3 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
|
4 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
- |
3 |
|
5 |
3 |
3 |
14 |
4 |
15 |
15 |
5 |
14 |
3 |
|
6 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
7a |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
|
8 |
6 |
6 |
6 |
6 |
6 |
6 |
10 |
6 |
6 |
|
9 |
14 |
14 |
14 |
14 |
14 |
14 |
13 |
13 |
13 |
|
10 |
4 |
4 |
5 |
4 |
2 |
5 |
5 |
5 |
4 |
Ce tableau reprend les durées propres à chaque série et les confronte, de façon à obtenir une synthèse optimale de la durée des vagues selon la méthode des moyennes mobiles (tout en gardant la série ip comme série privilégiée)
La synthèse des vagues qui ont abouti à une crise de surproduction nous donne une durée moyenne d’environ 5 trimestres avec un écart type de l’ordre de 3 trimestres. La durée la plus longue enregistrée est de 15 trimestres et de 13 trimestres pour la synthèse des moyennes mobiles. Les données ne constituent pas un échantillon représentatif.
Nous retrouvons les calculs de moyenne et d’écart type que nous avons présentés au chapitre 18.2 du livre sur le cycle des crises aux Etats-Unis depuis 1929.
2.2 Les vagues d’accélération selon la méthode des courbes de tendance
Les calculs à partir des courbes de tendance pour l’ensemble des séries et pour chaque cycle sont présentés dans le tableau suivant :
Le premier calcul, noté A, est fait à partir des données qui vont de l’origine de la courbe au trimestre qui suit le point de retournement de la période d’accumulation. Le second calcul, noté B, prend en compte la série des données jusqu’au trimestre de confirmation de la vague d’accélération selon la méthode des moyennes mobiles.
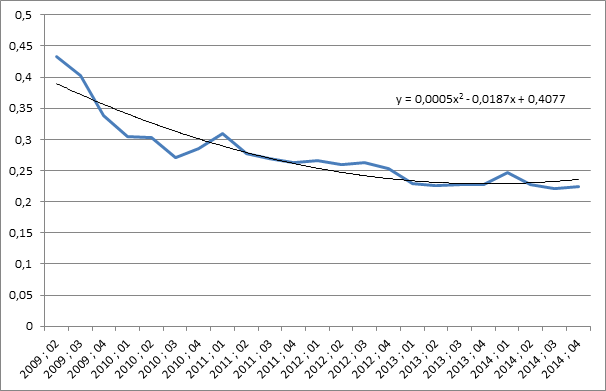
Il nous faut ici signaler une source d’erreur qui, jusqu’à présent, nous avait échappé. Il nous est arrivé de faire des calculs sur la base de courbes relatives de manière à pouvoir les comparer plus facilement sur un même graphique. Par exemple, dans notre dernier texte révisant la prévision, nous avons utilisé le graphique suivant :
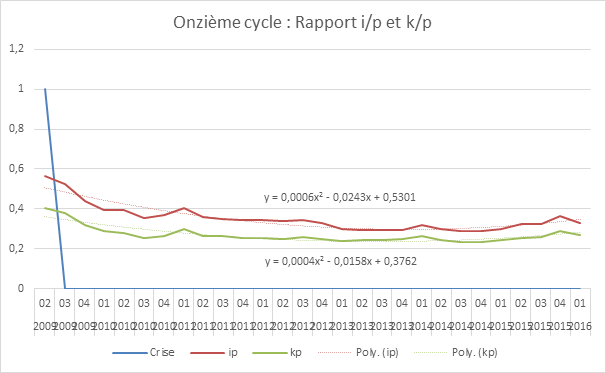
Les données propres au rapport i/p ont été systématiquement multipliées par 1,3 et celles du rapport k/p divisée par un coefficient légèrement supérieur à 4. L’allure de la courbe est identique mais l’algorithme de calcul de l’équation donne des résultats différents. Si nous revenons aux données de base nous obtenons une autre équation et le calcul de la courbe de tendance pointe sur le premier trimestre 2016, comme point départ de la vague d’accélération (cf. annexes). La prévision se déplace donc de deux trimestres. Cela signifie que nous sommes entrés dans la zone de plus grande probabilité de crise. La crise devrait donc se manifester entre le quatrième trimestre 2016 et la fin 2018 au plus tard.